COVID-19 / 東京星に、いこう

2020年5月4日

私、生まれも育ちも工学です。人呼んで煙人計画と発します。とかく数学に行きましても、医学に行きましても、分野分野のお兄貴さんお姐さんにごやっかいかけがちになるアラフォーです。以後、見苦しき文体お見知りおかれまして、向後万端ひきたってよろしくおたの申します。

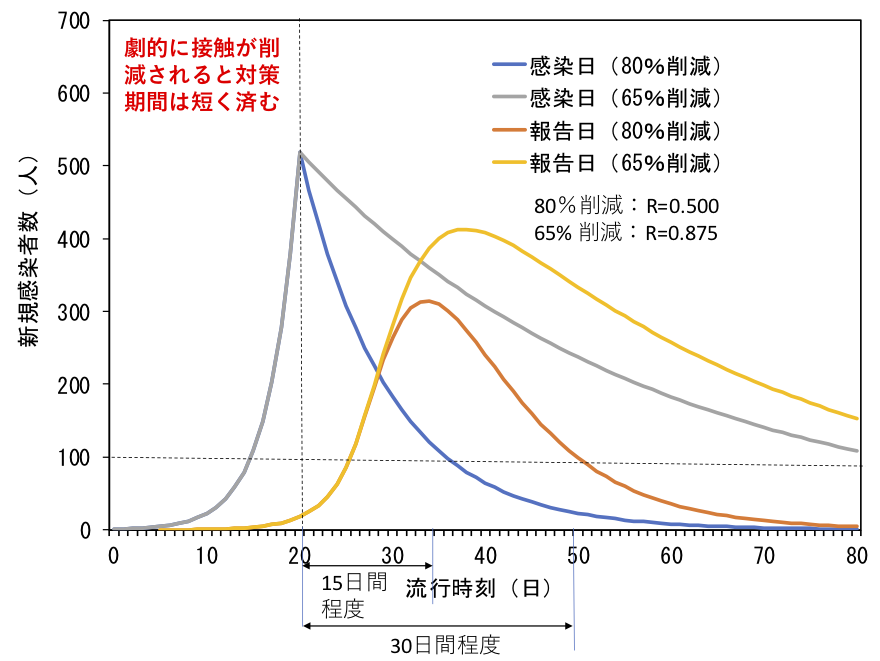
本稿では、新型コロナウイルス感染症対策専門家会議による「新型コロナウイルス感染症対策の状況分析・提言」（2020年4月22日）のP.3のポンチ絵（図1）を《リバースエンジニアリング》する。

図1 新型コロナウイルス感染症対策専門家会議による「新型コロナウイルス感染症対策の状況分析・提言」（2020年4月22日）のP.3のポンチ絵

「新型コロナウイルス感染症対策の状況分析・提言」（2020年4月22日）は、PDF形式で厚生労働省のウェブページに公開された。メタ情報によれば、「菱谷 文彦 (hishitani-fumihiko)」によって「2020/04/22 19:13」に「Microsoft© Word 2016」でPDFが作成されたらしい。

点線

1999年の東京ナロードニキ大学（註1）の卒論発表会で、このようなポンチ絵をプレゼンテーションしたら、舟をこいでいた学科長がクワッと眼を見ひらき、「どうして点線が傾いているのですか？」と即座に落第を言いわたされただろう。

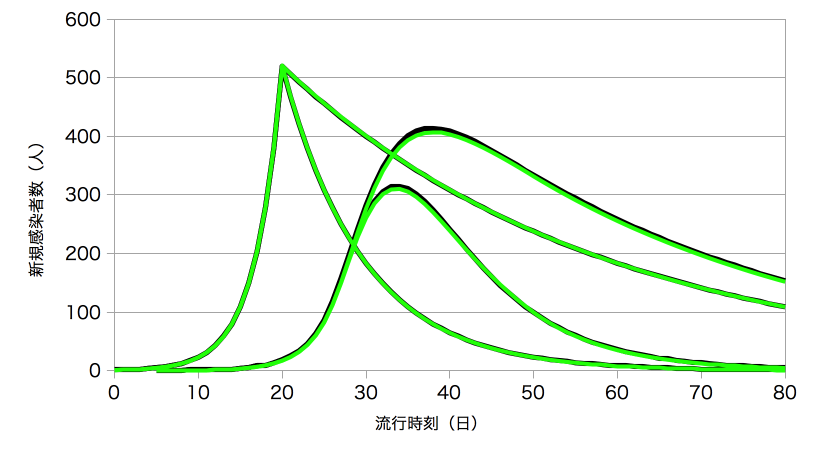
わかりやすいように図1のポンチ絵に垂直・水平の緑色のガイド線を追加した（図2）。曲線の端点が横軸の目盛りと目盛りのまんなかに位置している以上、縦の点線は横軸の目盛りと目盛りのまんなかを通らなければならない。だけど、そうはなっていないんだ。

図2 図1のポンチ絵に垂直・水平の緑色のガイド線を追加した。

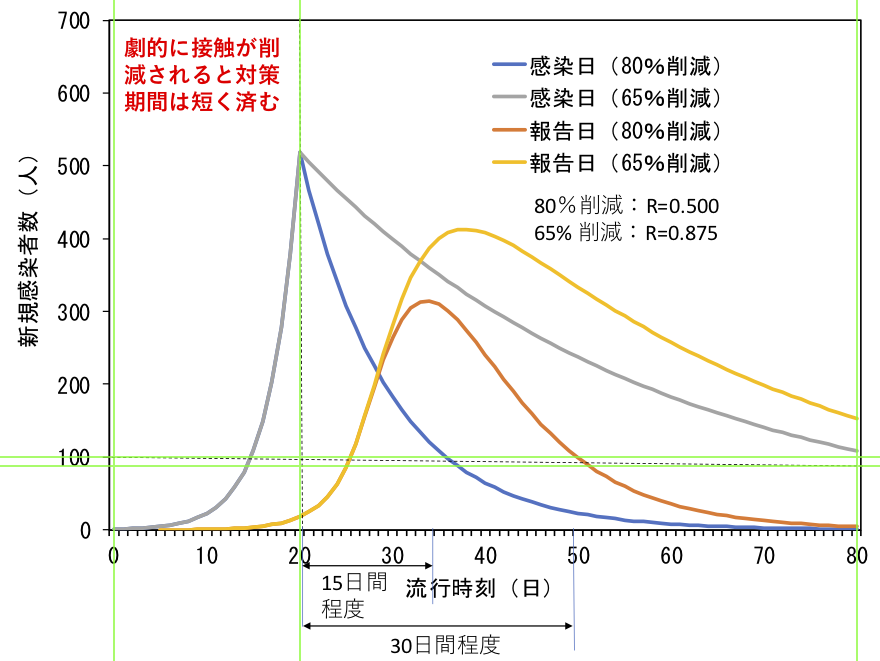
横の点線は80日で1割以上減少している。あまりに傾きすぎてはいないか。「新型コロナウイルス感染症対策の状況分析・提言」（2020年4月22日）の注釈は、「1日100人」という基準を用いて説明している。つまり、横の点線が水平であるべきことを示唆している。

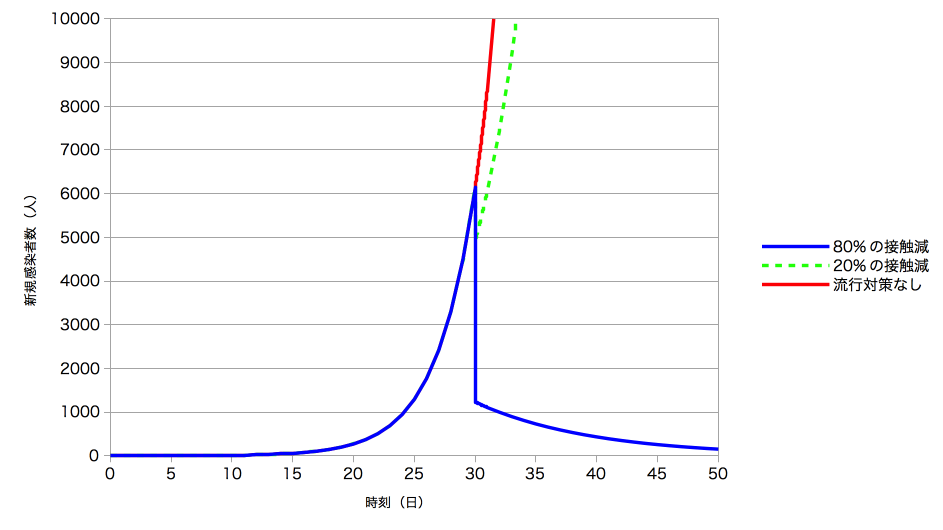
流行対策開始前までは\(\mathcal{R_0}=2.5\)で感染者数が増加する。感染日別の新規感染者数は80％の接触削減により15日間で1日100人まで減少する（青線）。しかし、接触の削減が65％であると1日100人に達するには9 日以上を要する（灰色線）。また、確定患者として報告されるにはおおよそ2週間の遅れを要し、80％削減のとき1日100人に到達するには緊急事態宣言から約1か月を要する（オレンジ線）。黄色線は65％削減のときの確定患者数である。

点線をあとから描きいれた人物は、感染症対策の、疫学の玄人であるが、グラフの素人である（註2）。

書体

書体にはくわしくないけれど、MSゴシックの箇所と游ゴシックとCalibriの箇所が混在していることはあきらかだろう（図3）。後者が、あとから書きいれられた箇所だろうことは容易に推測できる。PERCENT SIGNとFULLWIDTH PERCENT SIGNの不統一も、あじわいぶかさが感じられる。

図3 図1のポンチ絵の游ゴシックとCalibriの箇所に緑色の角丸四角形を追加した。

点列

PDFをInkspaceで読みこみ、不要な部分を削除してSVGで出力して、曲線を構成する点列を抽出した（抽出結果）。各点の局所座標をながめると、どこかの段階で量子化された痕跡を感じる（Wordに貼りつけた段階かもしれないし、WordからPDFを出力した段階かもしれないし、それらとは別の段階かもしれない）。

感染日別

抽出結果によれば、感染日別の新規感染者数は0日めにおおよそ1人、20日めにおおよそ520人であるらしい。仮に、仮にだけど、感染日別の新規感染者数を\(I(t)\)とおくと、20日め以前は、 \[ I(t) = e^{0.3127t} \quad (0 \le t \le 20, \mathcal{R} = 2.5) \] でほどよく再現できる。21日め以降も、 \[ I(t) = \begin{cases} 520 e^{-0.1042(t-20)} &(t \gt 20, \mathcal{R} = 0.5) \\ 520 e^{-0.0261(t-20)} &(t \gt 20, \mathcal{R} = 0.875) \\ \end{cases} \] でほどよく再現できる。\(\gamma \approx 0.2085\)とおくと、 \[ I(t) = \begin{cases} e^{\gamma (\mathcal{R} - 1) t} &\, (0 \le t \le 20) \\ 520 e^{\gamma (\mathcal{R} - 1) (t - 20)} &\, (t \gt 20) \\ \end{cases} \tag{1} \] でほどよく再現できる。どこかで見たような気がするんだけど、どこで見たんだっけ（回収される伏線）。

報告日別

感染日（80%削減）の青線の積算と、報告日（80%削減）のオレンジ線の積算は、ほとんど等しい。つまり、感染日別の新規感染者数にてきとうな確率分布をかけてあげると、報告日別の新規感染者数が出てきそうな按配だ。抽出結果を観察すると、\(t\)日めの感染日別の新規感染者数が、\(t+5\)日めの報告日別の新規感染者数にほとんど影響していないことがわかる。

報告日別の新規感染者数を\(J(t)\)とおいて、\(u\)日後への影響を\(a_u\)で与えると、 \[ J(t) = \sum_{u} a_u I(t + u) \] 数学にはくわしくないけれど、これくらいの連立方程式なら根性で解けそうな気がする（図4の青線）。金融工学あたりで見たことがある気がする線が出てきたので、てきとうに対数正規分布をあてはめた（図4の赤線）。\(\sigma = 0.5\)として、3日めから29日めまでで累積が99%になるように調節して、それらしさをかもしだした。

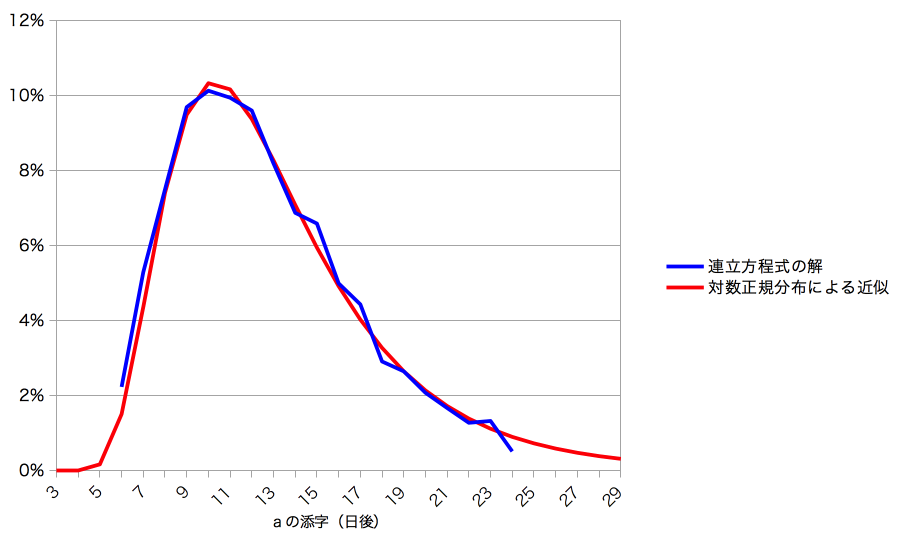
図4 感染日別の新規感染者数から報告日別の新規感染者数をもとめるための確率分布

感染の5日めから感染者が報告されはじめ、最頻値が10日めごろ、中央値（累積で50%が報告されるの）が11.5日めごろ、累積で90%が報告されるのが19.5日めごろという分布である。

再現

感染日別の新規感染者数については最大1.5人程度、報告日別の新規感染者数については最大8人程度ずれた（図5）。確率分布のつめに甘さがあることはいなめない。

図5 抽出した点列を太い黒線で描き、そのうちから計算で再現した点列を緑線で描きいれた。黒線があらわなところほどずれがおおきい。

SIRモデル

SIRモデルは常微分方程式系によって以下のように与えられる（西浦 and 稲葉, 2006）。 \[\begin{aligned} \frac{dS(t)}{dt} &= - \beta S(t) I(t) \\ \frac{dI(t)}{dt} &= \beta S(t) I(t) - \gamma I(t) \\ \frac{dR(t)}{dt} &= \gamma I(t) \\ \end{aligned}\] 全人口\(N = S(t) + I(t) + R(t)\)、再生産数\(\mathcal{R}=\frac{\beta N}{\gamma}\)とおくと、 \[ \frac{ dI(t) }{ dt } = \gamma \left( \mathcal{R} \left( 1 - \frac{I(t) + R(t)}{N} \right) - 1 \right) I(t) \] \(N\)がとてもおおきいとき、 \[\begin{aligned} \frac{ dI(t) }{ dt } &= \gamma \left( \mathcal{R} - 1 \right) I(t) \\ I(t) &= I_0 e^{\gamma (\mathcal{R} - 1) t} \\ \end{aligned}\] 奇妙なほどに式(1)と似かよっている。こんなに似ているということは、なにか意味があるのではないか。そのように考えたものたちがあったのは、ごく自然のなりゆきだろう。

ラベルをつけまちがえた可能性

その可能性はない。

点線をろくに引くことができないのだから、もちろん、ラベルをつけまちがえた可能性はいなめない。しかし、ラベルの書体はMSゴシックであり、つまり、あらかじめラベルづけされていたのだ。そもそも、SIRモデルの\(I(t)\)を定義どおりに解しているとき、てきとうな確率分布でぼかしたら、フィジカルな意味がよくわからなくなってしまわないだろうか。

初手から\(I(t)\)で新規感染者数を計算している可能性

その可能性はない。

「新型コロナウイルス感染症対策の見解」（2020年3月2日）の4節のポンチ絵の感染日別患者数において、緊急事態宣言直後に不連続性を見てとれる。2020年4月4日の@ClusterJapan氏のツイートの動画では、SIRモデルの\(-\frac{dS(t)}{dt}\)とおぼしき曲線を説明に供している（図6）。

図6 2020年4月4日の@ClusterJapan氏のツイートの動画のキャプチャ画像

なにしろ、\(\gamma \approx 0.2085\)を用いてSIRモデルの\(-\frac{dS(t)}{dt}\)を計算すると、奇妙なほどに図6が再現できてしまうのだ（図7）。ふしぎだなぁ（回収されない伏線）。

図7 \(\gamma \approx 0.2085\)を用いてSIRモデルの\(-\frac{dS(t)}{dt}\)を計算した。

2020年4月4日の11日後、2020年4月15日の@ClusterJapan氏のツイートで図1とほとんどひとしいポンチ絵が呈示された。

専門家や官僚や政治家が誤っている可能性

その可能性はない。

図6のポンチ絵では新規感染者数が急激にさがりすぎるので、愚鈍で蒙昧な大衆を恐怖させることができない。かかるがゆえに実効再生産数がじゅうぶんにさがらない。そのように4月6日から4月15日のどこかで専門家や官僚や政治家が考えたのではないか。

愚鈍で蒙昧な大衆を啓蒙し、教導するべく、数理モデルは転進しなければならなかった。専門家や官僚や政治家はけっして誤らない。誤るのはいつでも大衆だ。この素晴らしい数理モデルに説明を（註3）。

註釈

註1
矢作俊彦の歴史改変ライトノベルに登場する大学の名称。本稿の著者は造兵学科に在籍していたという設定。
註2
平野耕太の異世界転生マンガのセリフのパロディ。
註3
暁なつめの異世界転生ライトノベルのタイトルのパロディ。
註4
この註はどこからも参照されていない。本稿が宣戦布告であることはいうまでもない。