COVID-19 / 贖いの聖者

2020年5月29日

アテンション・プリーズ。このフィクションは数式です。あらゆる工学はロマンスなので、登場する団体名、会社名、及び個人名と現実のそれらとは一切関係がないなどと誰に断ずる権利があるでしょう

実効再生産数

実行再生産数の数式と実装が公開された。数式と実装のほとんどは、めんどうな現実に対応するために費やされている。感染日と発病日と診断日と報告日のずれや、輸入例と国内例の区別といった現実に対応するために。もちろん、そして高速化のために。

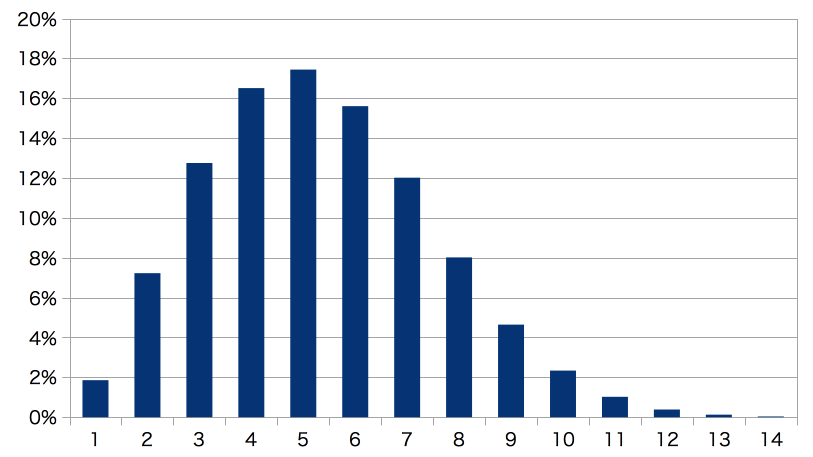
めんどうな現実から目をそらそう。時刻\(t\)における感染日別の新規感染者数を\(i(t)\)、実効再生産数を\(\mathcal{R_t}\)、世代間隔の確率密度関数を\(g\)とおくと、 \[ i(t) = \mathcal{R_t} \sum^{t-1}_{\tau=1} i(t-\tau) g(\tau) \tag{1} \] 昨日以前の新規感染者数に確率的な世代間隔をかけて合計する。さらに実効再生産数をかけると、今日の新規感染者数になる。世代間隔の確率密度関数はワイブル分布で与えられている（図1）。 \[\begin{aligned} m &= 2.345 \\ \eta &= 5.452 \\ F(\tau) &= 1 - \exp\left\{-\left(\frac{\tau}{\eta}\right)^m\right\} \\ g(\tau) &= F(\tau) - F(\tau-1) \\ \end{aligned}\] \(m\)と\(\eta\)はNishiuraら, 2020からやってきたらしい。

感染日別の新規感染者数がわかっていたら、実効再生産数が、いかんともしがたくもとまってしまう。式(1)はそういう式だ。

八割の抒情詩

前稿で新型コロナウイルス感染症対策専門家会議による「新型コロナウイルス感染症対策の状況分析・提言」（2020年4月22日）のP.3のポンチ絵（図2）を《リバースエンジニアリング》した。

ここには、感染日別の新規感染者数のデータがある。感染日別の新規感染者数がある以上、実効再生産数が、いかんともしがたくもとまってしまう（図3）。20日めまでは実効再生産数が4.27程度で、10日程度かけてじょじょにさがっていく。80%削減では実効再生産数が0.56程度に、65%削減では実効再生産数が0.87程度におちついていく。

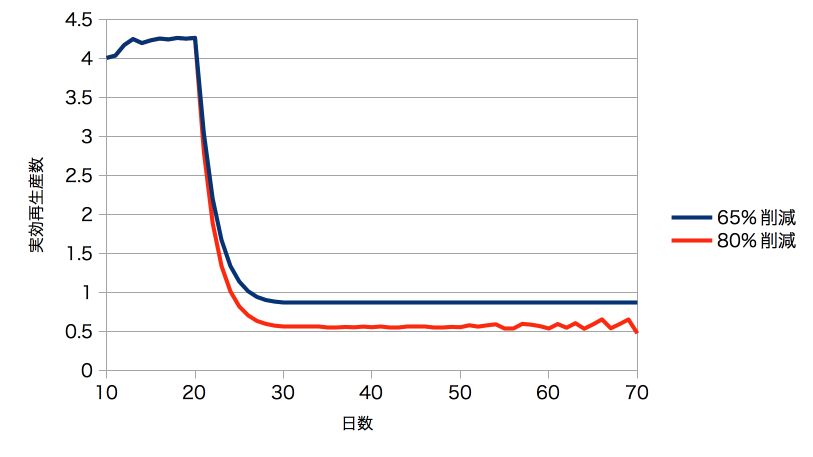
あれ？　あれれ？　なんかおかしくない？

八割の叙事詩

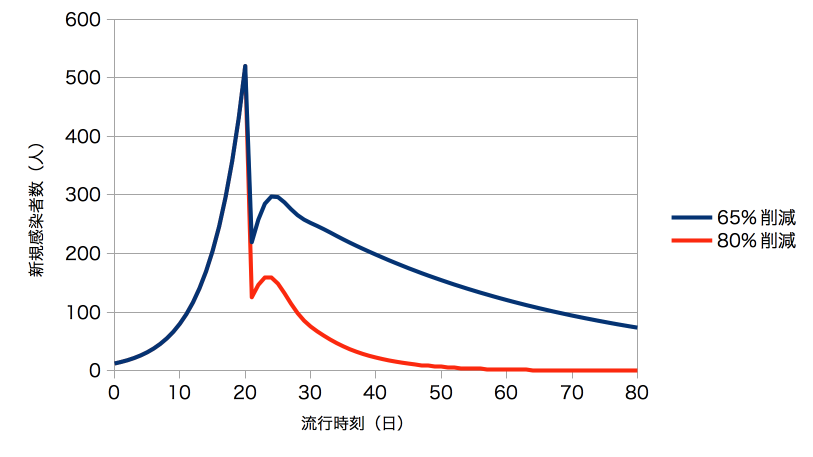
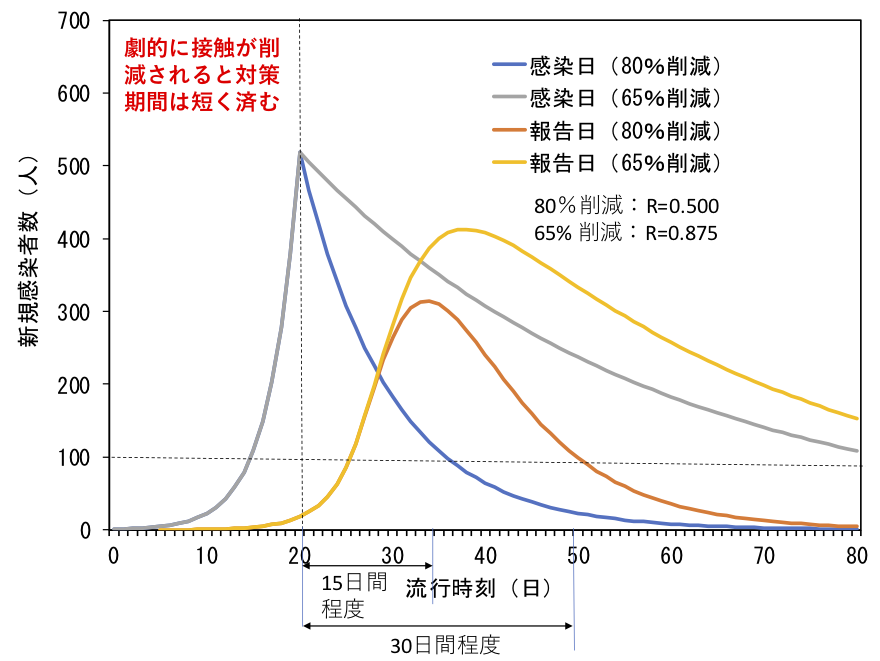
20日めまで\(\mathcal{R_t}=2.5\)で感染者数が増加し、20日めの新規感染者数がちょうど520人になる。21日めに接触機会が劇的に削減され、以降、65%削減ならば\(\mathcal{R_t}=0.875\)に、80%削減ならば\(\mathcal{R_t}=0.5\)になる。そんなありえたかもしれない感染日別の新規感染者数のポンチ絵を図4に示す。28日めには新規感染者数が100人をしたまわるような、これは計算だ。

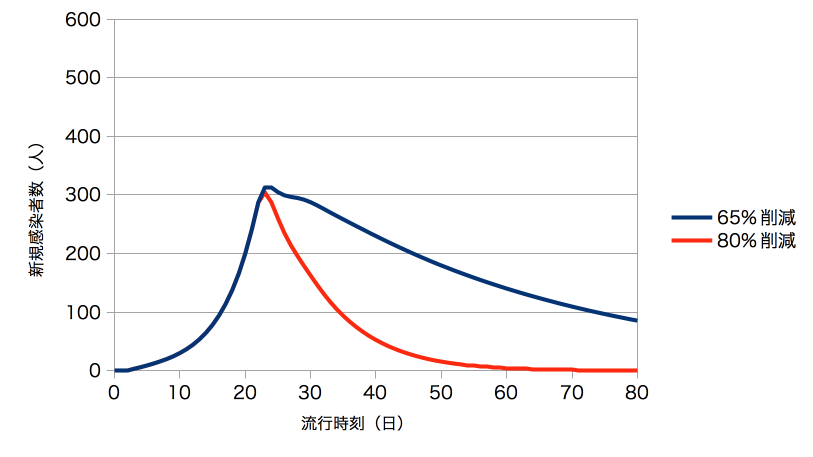
めんどうな現実に目をむけよう。潜伏期間は対数正規分布で与えられているから、ありえたかもしれない発病日別の新規感染者数を計算できる（図5）。

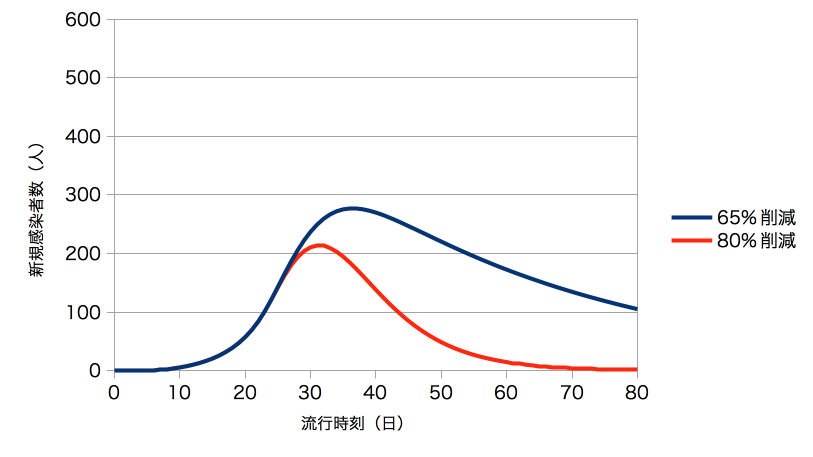
同様に診断日別の新規感染者数も計算する（図6）。

八割の神話とは、《バックプロジェクション》という時制の、つまり、物語なのだ。